In the previous case of a 500 cm³ cylinder, the ratio of the radius to the height was

1:2

when the surface area was at its minimum. As it turns out, this remains the case for cylinders of other volumes. The easiest way to show this is through several other examples to show this constant trend. In addition to the cylinder used in part 1, cylinders of volumes

50, 400, and 713,658 cm³

were put to the test. The equations for their surface area are as follows: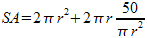
, , and .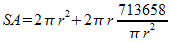
In the same manner, these are then graphed to find the optimal point where surface area is the least.



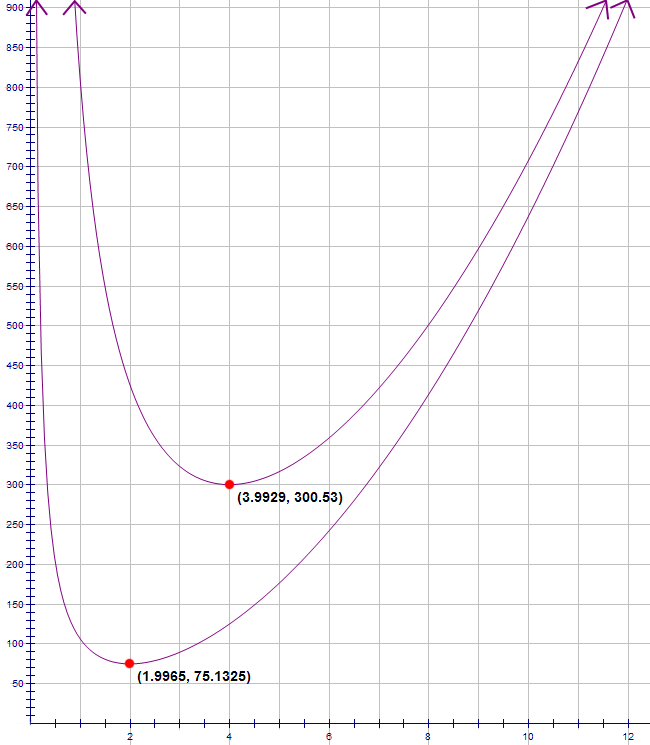
In the first example, the radius comes to

1.9965 cm

, the height is calculated to be

3.9928 cm

, and the surface area is

75.1325 cm²

.
In the next one, the radius is

3.9929 cm

, the height is

7.9861 cm

, and the surface area is

300.53 cm²

.
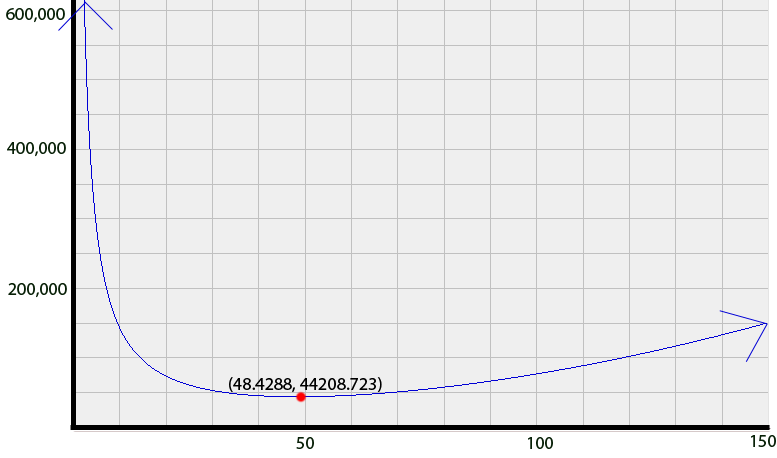
The trend even holds true if you needed to design an optimal cylinder for a large-scale industrial task, such as housing nuclear waste. This massive cylinder would have a radius of

48.4288 cm

, a height of

96.8574 cm

, and a surface area of

44,208.723 cm²

.

The three ratios are: 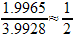, , 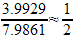and .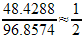

In every case, it is clear that the ratio of the radius to the height is about 1:2. In fact, it would be exact if not for prior rounding.